Die MAXWELL’sche Elektrodynamik

- einmal anders -

(Fassung vom 18. September 2002)

a) Vorbemerkungen

Jede Ableitung einer mathematischen Formel muss von einem oder mehreren Axiomen ausgehen. Ein Axiom ist eine Festsetzung, die selbst weder bewiesen noch widerlegt werden kann. Das gilt auch für mathematische Formeln zur Beschreibung physikalischer Sachverhalte. Im Verlaufe einer wissenschaftlichen Entwicklung ist es jedoch zulässig, Axiome zu ersetzen, wenn sich die bisherigen Axiome als unzweckmäßig erweisen.

Bei den beiden MAXWELL’schen Gleichungen, dem Kernstück der seit mehr als 100 Jahren in der Theoretischen Physik gelehrten Elektrodynamik, sucht man - auch in den Originalarbeiten von MAXWELL - vergeblich nach grundlegenden Axiomen. Es werden die beiden MAXWELL’schen Gleichungen, die unter dem Deckmantel der Symbole „rot H“ und „rot E“ sehr komplizierte mathematisch Differentialausdrücke verbergen, selbst wie Axiome behandelt und als weder beweisbar noch widerlegbar unterstellt. In folgendem soll untersucht werden, welches die eigentliche Grundlage der MAXWELL’schen Gleichungen ist.

In der Literatur zur theoretischen Elektrodynamik, beispielsweise bei POHL, R. W. (1967): „Elektrizitätslehre“, Verlag Springer, Berlin, Heidelberg, New York, 20. Auflg., Seiten 80/81 und 142/143, findet man folgende zwei Formeln (Vektorprodukte):

(101) H = D × u

(102) E = u × B

Hierin sind dreidimensionale Vektoren durch fett/kursiv-Druck, z. B H, D, E und B, gekennzeichnet, und zwar bedeuten E bzw. H die elektrische bzw. magnetische Feldstärke, D die dielektrische Verschiebung, B die magnetische Induktion, u den Vektor einer beliebigen Geschwindigkeit und × den Operator für das Vektorprodukt.

Im folgenden wird gezeigt, dass aus den Vektorprodukten (101) und (102) die homogenen Gleichungen der MAXWELL’schen Elektrodynamik ohne zusätzliche Annahmen abgeleitet werden können. Die homogenen Gleichungen werden als allgemeingültig angesehen für den gesamten elektromagnetischen Feldraum, in dem keine elektrischen Ladungen (Raumladungsdichte = 0) und/oder elektrischen Ströme (Konvektionsstromdichte = 0) vorhanden sind. Diese homogenen Gleichungen lauten in der Rotor-Schreibweise:

(1) rot H = + ¶ D / ¶ t

(2) rot E = - ¶ B / ¶ t

Die Gleichungen (101) und (102) stellen somit die eigentliche Grundlage der MAXWELL’schen Elektrodynamik dar.

b) Mathematische Ableitung

Um die „Rotor-Operation“ in den Gleichungen (1) und (2) durchführen zu können, betrachten wir die Gleichungen in der ausführlichen, differentiellen Form. Die homogenen Maxwell’schen Gleichungen in kartesischen Koordinaten (x, y, z) lauten wie folgt (Komponenten der Vektoren werden durch einfache Kursivschrift gekennzeichnet, z. B. H_x, H_y, H_z,):

(1a) [ ¶ H_z / ¶ y ] - [ ¶ H_y / ¶ z ] = [ ¶ D_x / ¶ t ]

(1b) [ ¶ H_x / ¶ z ] - [ ¶ H_z / ¶ x ] = [ ¶ D_y / ¶ t ]

(1c) [ ¶ H_y / ¶ x ] - [ ¶ H_x / ¶ y ] = [ ¶ D_z / ¶ t ]

(2a) [ ¶ E_z / ¶ y ] - [ ¶ E_y / ¶ z ] = - [ ¶ B_x / ¶ t ]

(2b) [ ¶ E_x / ¶ z ] - [ ¶ E_z / ¶ x ] = - [ ¶ B_y / ¶ t ]

(2c) [ ¶ E_y / ¶ x ] - [ ¶ E_x / ¶ y ] = - [ ¶ B_z / ¶ t ]

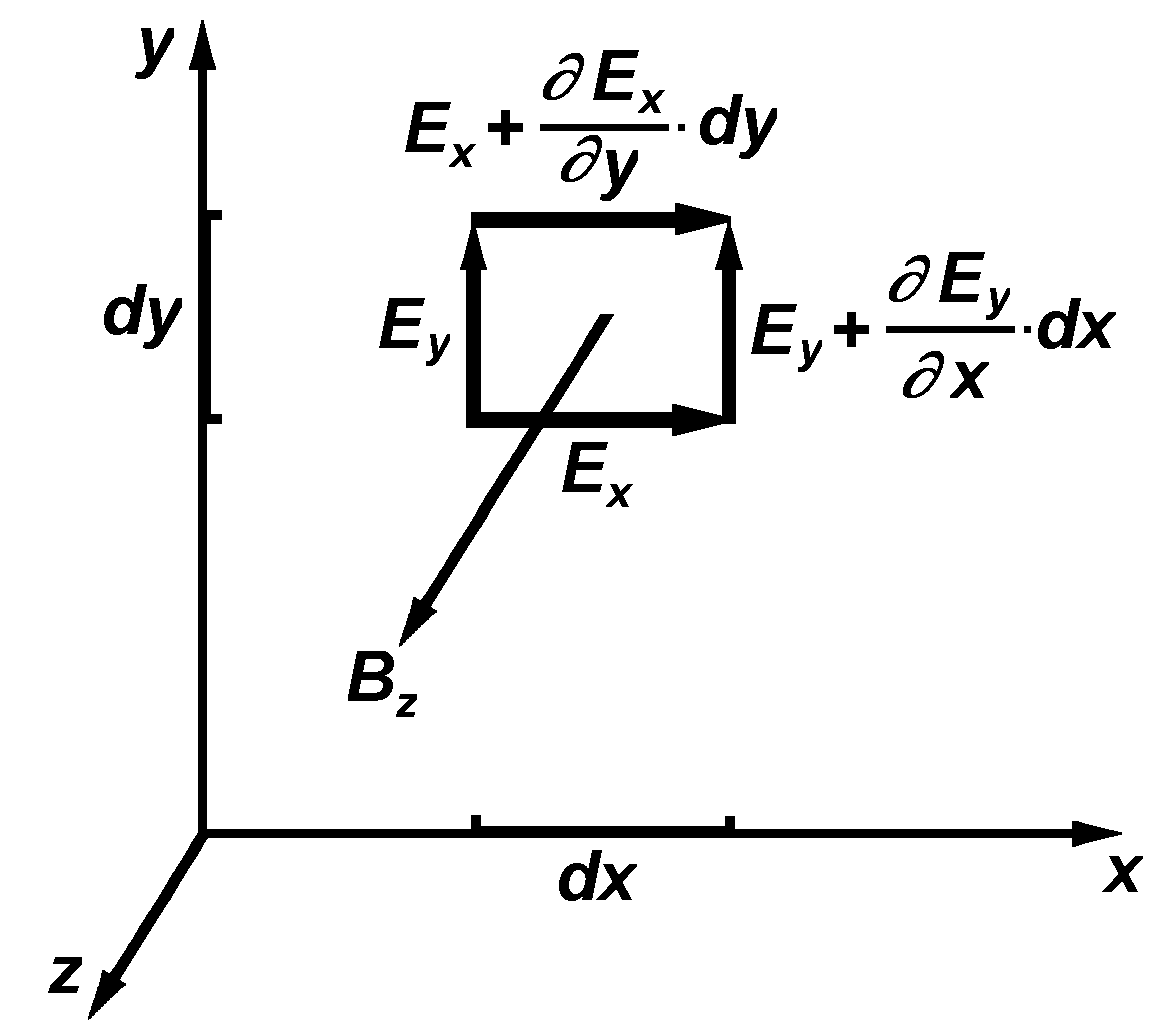
Bild 1

Wir betrachten zunächst die Gleichungen (102) und (2). Angenommen wird ein Flächenelement mit den differentiellen Abmessungen dx und dy in einem rechtwinkligen, kartesischen Koordinatensystem entsprechend Bild 1. Die in Bild 1 eingetragenen Pfeilrichtungen kennzeichnen die mathematisch positiven Richtungen. Die magnetische Induktion B_z = B_z(t) wird in der positiven z-Richtung angenommen.

In einer Art Definition bilden wir nun - in Anlehnung an Wilhelm H. Westphal: „Physik“, 13. Auflg. (1948), Springer-Verlag, § 232 (Seiten 417 bis 419) - die elektrische Umlaufspannung U₀ auf dem Umfang des Flächenelementes, indem wir einen vollen Umlauf im mathematisch positiven Sinne um die z-Achse ausführen. Wir erhalten (siehe Bild 1):

(3) U₀ = E_xdx + { E_y + [¶ E_y / ¶ x] dx } dy - { E_x + [¶ E_x / ¶ y] dy } dx - E_ydy

(4) U₀ = { [¶ E_y / ¶ x] - [¶ E_x / ¶ y] } dx dy

Hiermit sind die räumlichen Komponenten der Gleichung (2c) definiert.

Nun muss noch die tatsächliche Umlaufspannung U₀ als Funktion des Geschwindigkeitsvektors u bestimmt werden.

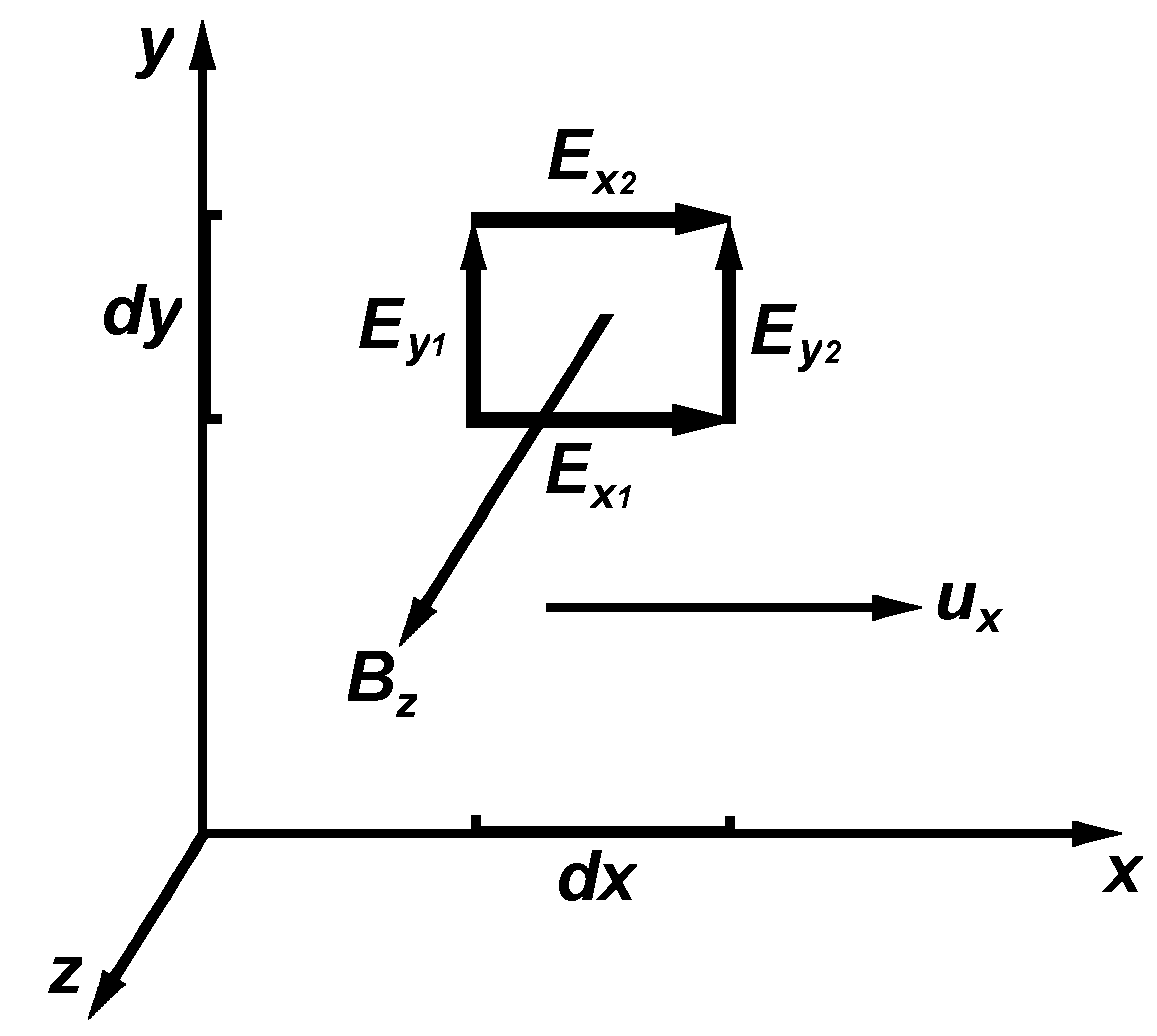
Bild 2

Erneut wird ein Flächenelement mit den differentiellen Abmessungen dx und dy in einem rechtwinkligen, kartesischen Koordinatensystem angenommen. Das Flächenelement liege in der x-y-Ebene gemäß Bild 2. Hierbei sind der Übersichtlichkeit halber andere Bezeichnungen für die Anteile der Umlaufspannung U₀ gewählt. Die in Bild 2 eingetragenen Pfeilrichtungen kennzeichnen wieder die mathematisch positiven Richtungen. Wieder ist die magnetische Induktion B_z = B_z(t) in z-Richtung angenommen. Der Vektor B_z ist gemäß der vorgegebenen Vektorgleichung (102) mit dem Geschwindigkeitsvektor u vektoriell verknüpft (Vektorprodukt).

Wir legen das Koordinatensystem so, dass die Richtung des Geschwindigkeitsvektors u mit der positiven Richtung der x-Achse zusammenfällt. Dann gilt:

u = u_x (siehe Bild 2).

Für ein Vektorprodukt gilt allgemein folgende Festlegung: Der Produkt-Vektor P steht senkrecht auf der Ebene der beiden Vektoren, welche die Faktoren (F₁ und F₂) des Vektorproduktes (P) bilden. Hierbei sind die Größen P, F₁ und F₂ keine Vektoren sondern skalare Beträge. Der Betrag des Produkt-Vektors (P) ergibt sich zu:

(5) P = F₁ • F₂ • sin î ,

wobei î den Winkel zwischen den Faktoren F₁ und F₂ darstellt. Dabei ist zu berücksichtigen, dass das Vorzeichen eines Vektorproduktes von der Reihenfolge der Faktoren abhängig ist.

Wir erhalten die elektrische Umlaufspannung U₀ auf dem Umfang des Flächenelementes, indem wir einen vollen Umlauf im mathematisch positiven Sinne um die z-Achse ausführen:

(6) U₀ = E_x1 dx + E_y2 dy - E_x2 dx - E_y1 dy

Da u_x parallel zur x-Achse liegt (d. h. Winkel î = 0^o), ergibt sich aus der Vektorgleichung (102)

(7) E_x1 = 0

(8) E_x2 = 0

Da andererseits u_x senkrecht zu dy liegt (d. h. Winkel î = 90^o), folgt ebenfalls aus Vektorgleichung (102):

(9) E_y2 = - u_x { B_z + [¶ B_z/ ¶ x] dx }

(10) E_y1 = - u_x { B_z + 0 }

und daraus als Umlaufspannung nach Gleichung (6):

(11) U₀ = 0 + E_y2 dy - 0 - E_y1 dy

(12) U₀ = - u_x { B_z + [¶ B_z/ ¶ x] dx - B_z.} dy

Daraus:

(13) U₀ = - u_x [¶ B_z/ ¶ x ] dx dy]

Für u_x gilt folgende zeitliche Ableitung:

(14) u_x = [¶ x / ¶ t ] ,

Zusammenführen von (13) und (14) ergibt:

(15) U₀ = - [¶ B_z/ ¶ x ] [¶ x / ¶ t ] dx dy]

(16) U₀ = - [¶ B_z/ ¶ t ] dx dy]

Gleichsetzen der Umlaufspannung U₀ der beiden Gleichungen (4) und (16) führt auf folgende Zuordnung:

(17) { [¶ E_y / ¶ x] - [¶ E_x / ¶ y] }dx dy = - [¶ B_z/ ¶ t] dx dy

Daraus:

(18) [¶ E_y / ¶ x] - [¶ E_x / ¶ y] = - [¶ B_z/ ¶ t]

Dies entspricht aber genau der eingangs genannten Gleichung (2c).

Aus Gleichung (18) erhalten wir dann die Gleichungen (2a) und (2b) durch zyklische Vertauschung der Indizes der Gleichung (18) in der Reihenfolge x - y - z – x.

In gleicher Weise können auch die Gleichungen (1a), (1b) und (1c) anhand der Bilder 3 und 4 abgeleitet werden.

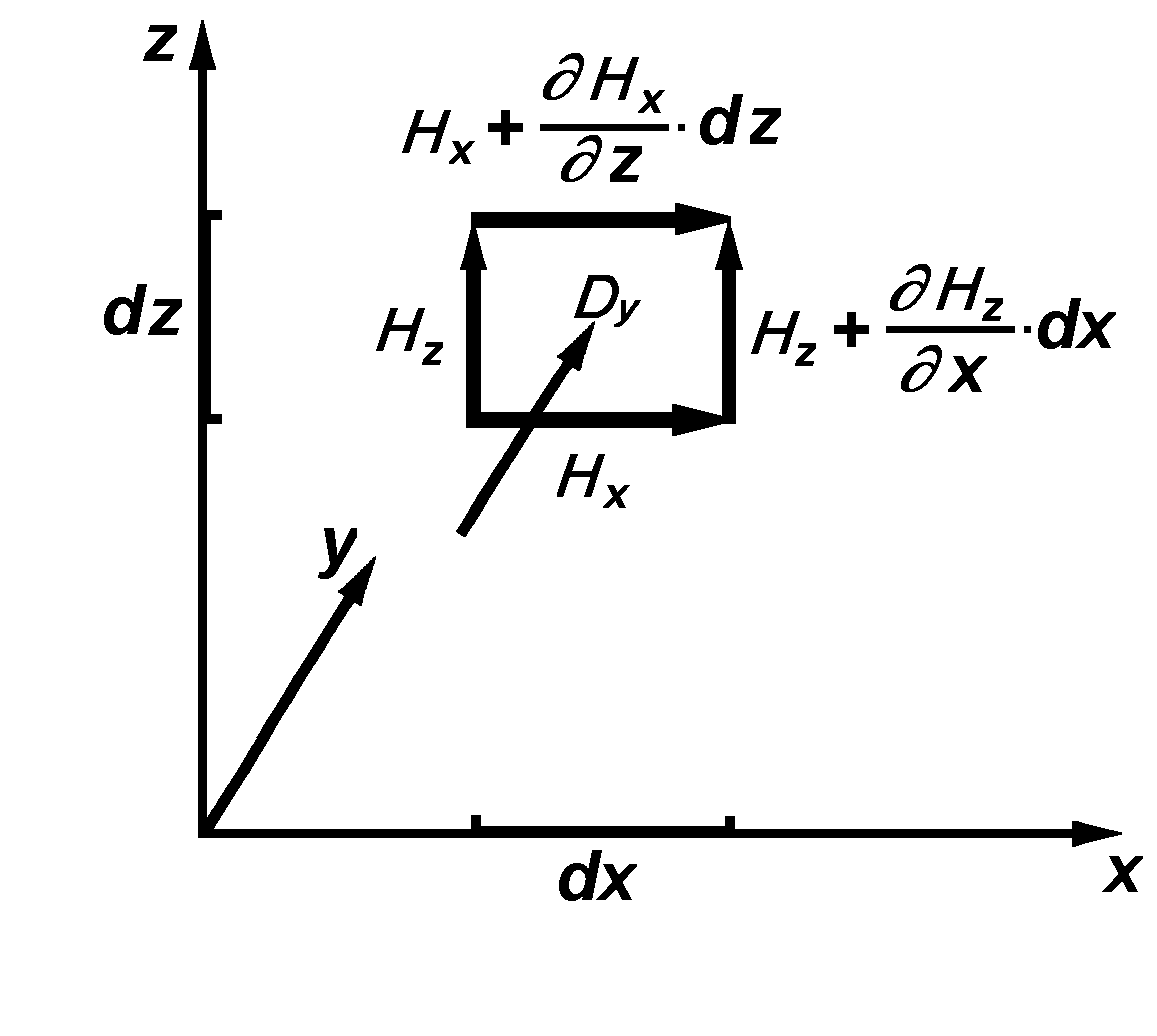
Bild 3

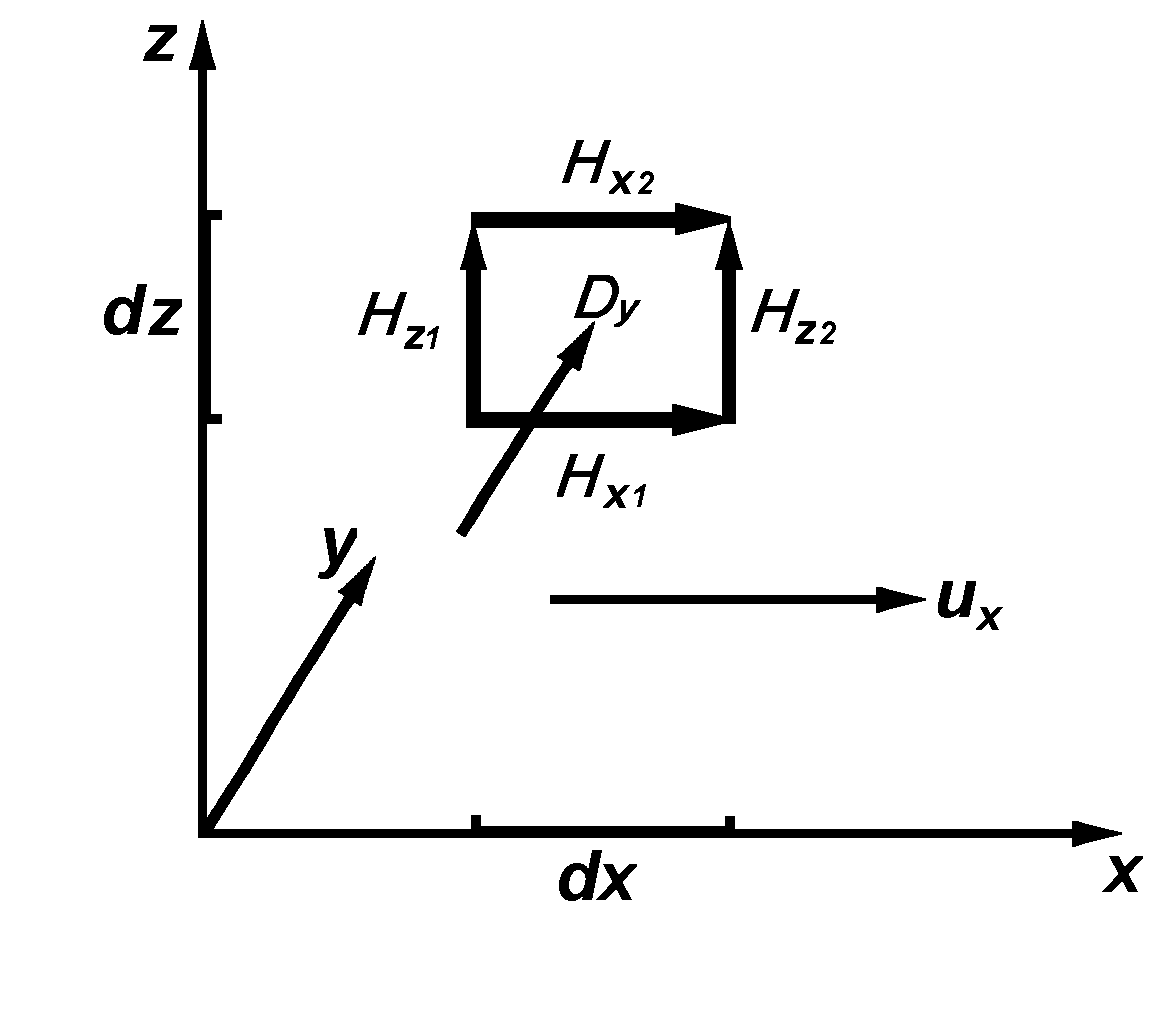
Bild 4

c) Schlußbetrachtung

Wie vorstehende Untersuchungen zeigen, lassen sich die homogenen Gleichungen der MAXWELL’schen Elektrodynamik ohne zusätzliche Annahmen ableiten aus folgenden Vektorprodukten:

(101) H = D × u

(102) E = u × B

Bemerkenswert ist dabei, dass der Geschwindigkeitsvektor u durch die „Rotor-Operation“ verloren geht. Die homogenen MAXWELL’schen Gleichungen haben daher einen geringeren Informationsgehalt als die Vektorprodukte (101) und (102). Man kann deshalb auch nicht umgekehrt die Vektorprodukte aus den homogenen Gleichungen mathematisch ableiten.

Außerdem kann gezeigt werden (vergl. hierzu: „Die Vektorprodukte der MAXWELL’schen Elektrodynamik“), dass die von MAXWELL vorgenommene Einführung der physikalischen Zuordnungen:

D = e₀E
und
B = m₀H
(mit e₀= Dielektizitätskonstante und m₀= Permeabilität des Vakuums)

zu grundlegenden Widersprüchen in der Elektrodynamik führt, da dadurch die beiden homogenen MAXWELL’schen Gleichungen in unzulässiger Weise miteinander verkoppelt werden (vergl. hierzu: „Sind Dielektrizität und Permeabilität des Vakuums Naturkonstanten?“).

[Home] [e-mail] [Autor] [Literatur]